Il nostro blog: foto, video e approfondimenti
Problemi (di matematica) in prima elementare: perché no?
- 05/12/2017
- Pubblicato da: Cecilia Sartini
- Categoria: MATEMATICA SCUOLA

Questo articolo è scritto con un duplice intento apologetico: da un lato vorrei difendere la grande potenza formativa della matematica, dall’altro vorrei spezzare una lancia a favore dell’intelligenza infantile, sempre pronta a soprendere noi adulti ormai ancorati alle nostre salde certezze.
Qualche tempo fa abbiamo pubblicato un lungo articolo sulle implicazioni connesse allo svolgere problemi nell’ora di matematica (https://www.associazionetokalon.com/problema-dei-problemi/). Oggi voglio offrirvi la sintesi di un’esperienza che nasce da una sfida: proporre problemi in classe prima elementare, sin dai primissimi giorni di scuola!
Ripercorrendo i miei ricordi di bambina, mi sono resa conto che svolgere problemi comportava per me una serie di pratiche estremamente distanti dalla mia sensibilità infantile:
- scrivere la parola Problema al centro della pagina;
- stendere il testo con la penna blu;
- la domanda invece con la penna rossa;
- elencare i dati, sul lato sinistro;
- inserire il termine Risolvo, sempre al centro della pagina;
- a sinistra scrivere in riga le operazioni, con tanto di didascalia in rosso per spiegare le entità su cui stavo operando;
- a destra incolonnare le operazioni, financo si trattasse di calcoli banali;
- al centro inserire un bel diagramma di flusso (di che flusso si trattasse, poi, non l’ho mai capito… per me, certamente un flusso di noia);
- scrivere la parola Rispondo al centro della pagina, seguita da una frase che chiarificava LA soluzione al problema;
- incrociare le dita e sperare che la soluzione da me individuata fosse QUELLA esatta (Verbum Domini – Deo gratias!).
Non credo che sia difficile riconoscere l’enorme distanza che esiste tra l’elenco precedente e la fantasiosa creatività di una bambina!
Quando, a inizio anno scolastico, mi è stata assegnata una classe prima, ho iniziato a guardarmi intorno e mi sono resa conto che, tra guide didattiche e metodi ormai universalmente considerati autorevoli (“La folla è la prova del peggio”, insegna Seneca), nessuno proponeva i famigerati problemi all’inizio del percorso scolastico; addirittura alcuni consigliavano di presentarli direttamente al secondo quadrimestre non solo in prima elementare, ma anche negli anni successivi!
Tuttavia, mossa dal “fuoco sacro della matematica”, ovverosia dalla fiducia nella sua potenza formativa (Platone docet…), mi sono lanciata nell’avventura e, in data 25 settembre 2017 ho proposto ai miei pargoli di prima il seguente problema, riadattato dal volume di A. Millàn Gasca Numeri e forme. Didattica della matematica con i bambini:
La famiglia di Pietro è formata dai genitori, da Pietro e dalla sorella Sara. La mamma ha comprato otto supplì per la cena di oggi. Quanti supplì toccheranno a ciascuno?
Ho introdotto il problema come se fosse una storia, mimando la mamma in pizzeria, e ho cercato di coinvolgere i bambini a livello della loro esperienza personale, permettendo loro di raccontare aneddoti sui supplì e realizzando un piccolo sondaggio sulla loro ghiottoneria in merito (ho anche scoperto che, in barba alla romanità, alcuni ignoravano completamente di cosa si trattasse!). Tutto ciò per favorire la mimesis nella situazione, in quanto, come insegna il nostro “caro amico” George Polya,
Un ingrediente essenziale del problema è il desiderio, la volontà e la decisione di risolverlo. Un problema diventa il vostro problema, lo possedete veramente, quando decidete di farlo, quando desiderate di risolverlo.
A questo punto siamo passati a dialogare sul problema, ipotizzando varie soluzioni: un’equa ripartizione del bottino (2 supplì a testa), oppure una distribuzione che rispettasse le differenti capacità degli stomaci (3 supplì agli adulti, 1 ai bambini), o ancora l’abnegazione di sé della figura materna, che cede uno dei supplì di sua pertinenza al papà (schema: 3, 2, 2, 1), o la golosità dei piccoli, che chiedono a ciascun genitore di regalare loro un supplì (sicché 3 supplì ai bambini, 1 agli adulti, con sovvertimento del naturale ordine degli stomaci)… Insomma, chi più ne ha, più ne metta! Al termine, ho chiesto ai miei alunni di realizzare un disegno della “storia”, attraverso il quale si capisse una modalità di distribuzione dei supplì. Riporto di seguito il lavoro di un alunno che ha prima di tutto disegnato l’eroica madre che procaccia il bottino alla famiglia (sul lato destro del foglio), quindi la distribuzione complessiva del cibo; da notare che il bambino ha spontaneamente evitato di raffigurare due supplì per ogni persona: si è limitato a scrivere il simbolo del numero 2 seguito da un piccolo cerchio a mo’ di supplì. Un primo passo verso l’astrazione!
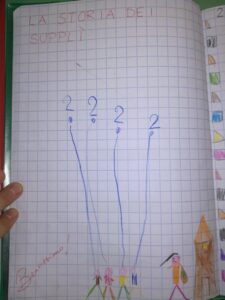
Nel corso dei mesi abbiamo continuato a divertirci con tante “storie problematiche”, e devo riconoscere che gli esiti sono stati sorprendenti: la mente infantile vede la realtà in modo “genuino”, profondo e spesso molto acuto, e riceve da una disciplina come la matematica una sollecitazione unica al ragionamento e in ultima istanza alla ricerca della verità.
Mi limito a riportare in fondo all’articolo qualche testo di problema e i corrispondenti disegni realizzati da alcuni bambini, lasciando a voi ulteriori considerazioni.
Vi invito anche a dare un’occhiata alla curiosa striscia che abbiamo inserito come immagine di copertina, tratta da una serie realizzata negli anni Venti da Antonio Rubino, celebre collaboratore de Il Corriere dei Piccoli.
Un saluto e… Buona Matematica a tutti!!
1. La mamma prepara un’ottima torta al cioccolato per i suoi quattro figli. Vuole darne due fette a testa. In quante parti dovrà tagliare la torta?

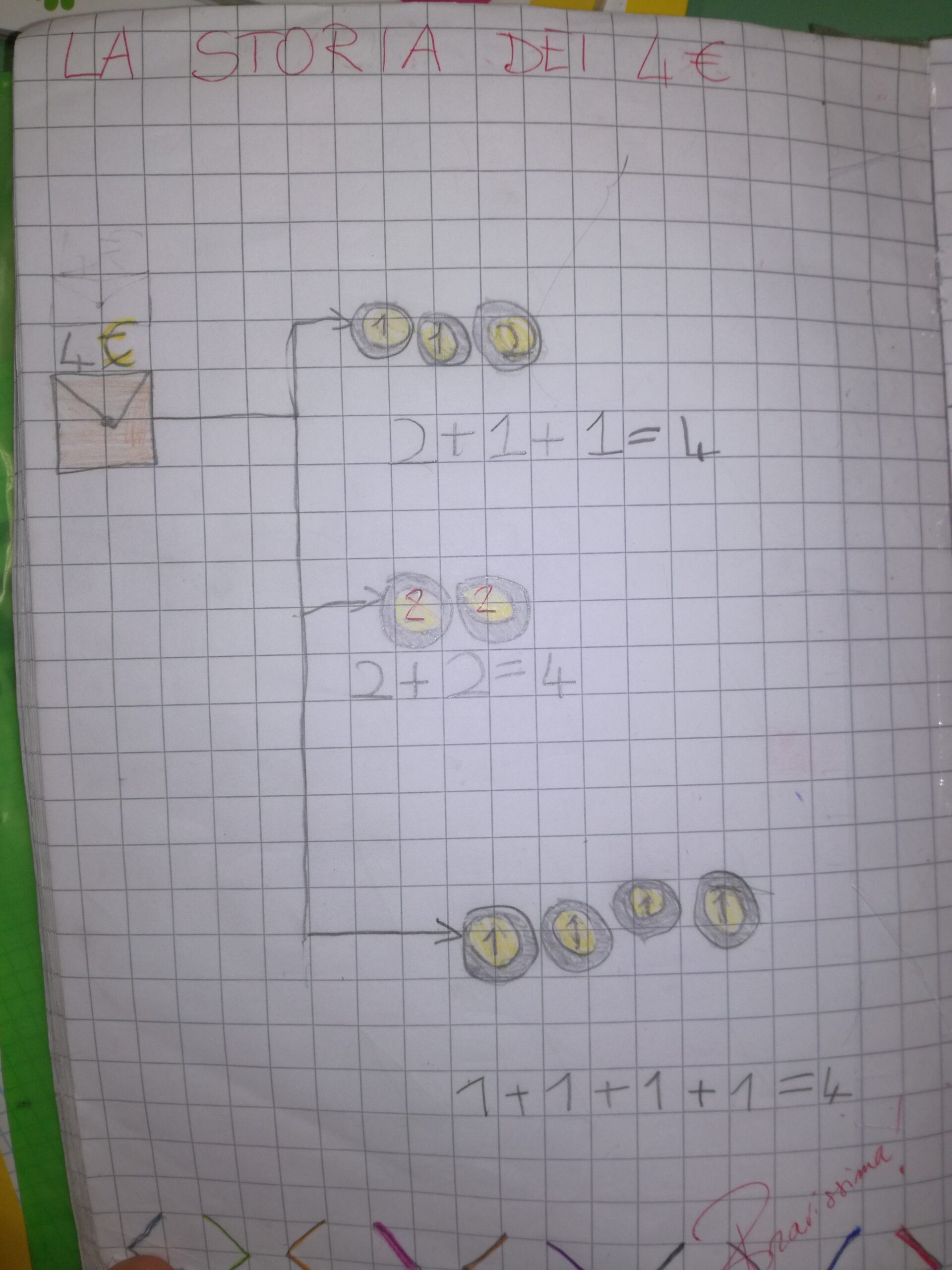
2. Nel mio portafoglio ci sono 4 euro, in monete da 1 euro, 2 euro, o miste. Quali le possibili combinazioni?
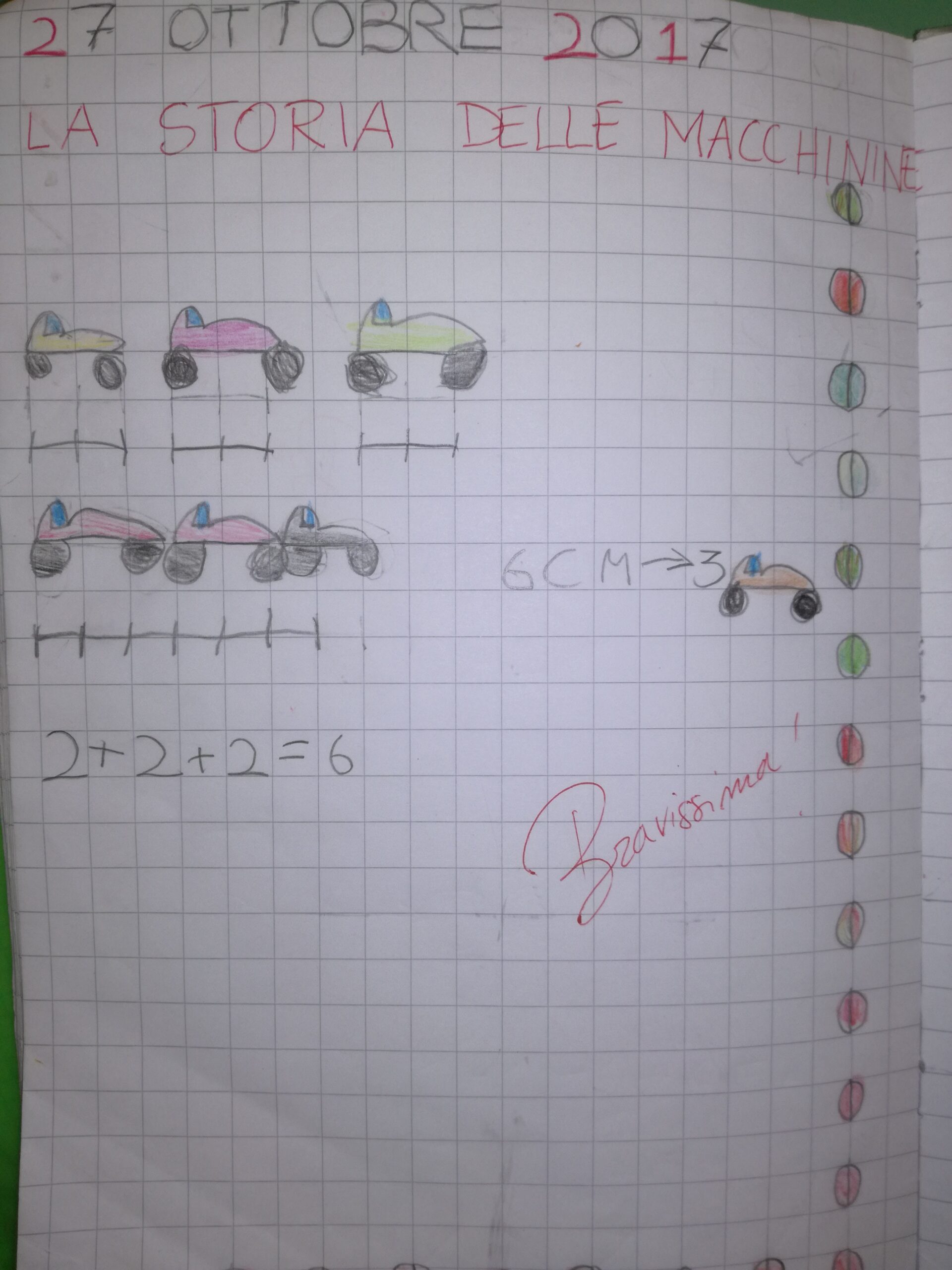
3. Giulio ha 3 mini-macchinine, ciascuna della lunghezza di 2 cm. Le mette in fila una dietro l’altra: quanti cm coprirà?
4. Giulia ha 6 caramelle, e due amiche con cui le divide.
Una prima soluzione proposta è stata: “Giulia tiene per sé 3 caramelle e consegna le restanti 3 alle amiche, che le dividono in questo modo: una ciascuno e la terza divisa a metà.”



5. La mamma va dal fornaio a comprare la pizza, spendendo 6 euro. Paga con una banconota da 10 euro. Quanto resto riceve?

NB: per altre immagini come quella in copertina cercate in rete Antonio Rubino e Il corriere dei piccoli… https://www.google.com/imgres?imgurl=https://flashbak.com/wp-content/uploads/2016/08/Antonio-Rubino-22Caro-e-Cora22-comic-Corriere-dei-Piccoli-1919-834×1024.jpg&imgrefurl=https://flashbak.com/antonio-rubino-cartoons-for-corriere-dei-piccoli-frank-sidebottom-hitler-youth-and-quadratino-362477/antonio-rubino-%2522caro-e-cora%2522-comic-corriere-dei-piccoli-1919/&docid=PiMEMPBCh_NMoM&tbnid=d2ChFNd-9_r38M&vet=1&w=834&h=1024&hl=it-IT&source=sh/x/im

Brava!
Anch’io lavoro così. Bello sapere di non essere fra le tante classiche maestre! Grazie
Bellissimi esempi, ottimo lavoro! Un piccolo appunto, sarebbe bello se le storie fossero un po’ meno piene di stereotipi di genere. Perché è sempre la mamma a cucinare o a comprare il cibo? Non può farlo anche il papà? Scusa se lo dico ma ricordo come questi stereotipi fossero ovunque nei testi di matematica dei miei figli alle elementari.
Bel lavoro!
Concordo tuttavia con Barbara: togliere gli stereotipi di genere sarebbe meglio! 😉