I dieci comandamenti di Polya

Matematica (e non solo), ecco il decalogo per insegnare bene

Da un recente studio dell’Ocse in merito alla correlazione tra successo scolastico in matematica e motivazione emerge che la maggior parte degli studenti italiani – oltre a non ottenere risultati particolarmente brillanti – non crede che un maggiore impegno possa migliorare il loro rendimento e solamente il 19% pensa che la matematica potrebbe dargli una marcia in più su un possibile lavoro futuro. In un articolo uscito di recente su Repubblica si prova ad individuare la ragione di questa difficoltà: “chi si impegna ottiene sempre risultati” afferma una docente di matematica in un liceo scientifico di Palermo; per un pedagogista e docente all’università di Firenze “i ragazzi non vedono l’applicabilità nella vita quotidiana della matematica, che considerano una materia astratta, e di conseguenza perdono l’interesse. […] Occorrerebbe invece costruire progetti educativi incentrati sull’interesse, ma nel nostro paese questo è un traguardo ancora piuttosto remoto”.

Stiamo affrontando un problema che riguarda il significato stesso dello studio, che coinvolge tutte le discipline di cui la matematica è solamente la punta dell’iceberg… Qual è il senso del nostro impegno? Perché vale la pena studiare? Perché matematica? C’è sempre meno senso del dovere e questo potremmo considerarlo un bene, in quanto così lo studente non si accontenterebbe di lavorare solo per portare buoni voti a casa… Anni fa alla domanda “perché studiare?” era frequente trovare una risposta come: “mio padre lavora tutto il giorno e porta i soldi a casa; io studio e devo portare i buoni voti a casa”. Oggi siamo nell’epoca storica dell'”A che cosa serve?” e, se oggi non basta dare una risposta “utilitaristica” a questa domanda, diventa ancora più attuale quanto affermava George Polya, un grande matematico ungherese che nel secolo scorso ha offerto un prezioso contributo alla didattica della matematica: “Immaginate di avere in classe un ragazzo bravo e intelligente, non ancora danneggiato dalla scuola, che ancora non vi tema, che in un qualsiasi momento potrebbe chiedervi, onestamente e ingenuamente: «Ma professore, a che serve questo?» Se cercate di figurarvi quello che c’è nella mente di quel bravo ragazzo e di programmare il vostro insegnamento in modo da poter rispondere a quella domanda critica – oppure in modo che egli si senta sempre divertito e sfidato e non abbia alcuna opportunità di porre quella domanda critica – potete diventare un insegnante migliore”.

E anche tra gli studenti c’è chi non si accontenta: “io studio per me, oggi, per crescere un po’ di più nella consapevolezza di chi sono e qual è il mio posto nel mondo”. Non si tratta di studiare matematica oggi perché mi servirà nel lavoro domani!

A tal proposito segnalo un prezioso intervento del prof. Underwood Dudley, What is mathematics for? (Notices AMS 57, 2010): “[…] il pubblico sa, o sente, che la matematica sviluppa il potere della ragione. Essa mostra, meglio di qualsiasi altro argomento, come la ragione può condurre alla verità. […] In matematica i problemi possono essere risolti usando la ragione, e le soluzioni possono essere controllate e mostrate corrette. A ragionare si deve imparare, e la matematica è il modo migliore di impararlo. […] Alle persone piace essere capaci di ragionare correttamente. Sanno che l’esercizio fa bene. Nessuno mi ha mai detto «Mi piaceva la matematica perché mi procurava un buon lavoro»”.

Come ho già avuto modo di osservare nella recensione del libro Pensare in matematica (G. Israel, A. Millan Gasca, Zanichelli 2012) si tratta di “restituire la matematica alla cultura”. Citando il grande matematico del secolo scorso Federigo Enriques: “l’acquisto della cultura suppone sempre l’apprendimento dell’uso che possa farsene; il quale esige la partecipazione attiva dell’educato, e ha un valore formativo”. Perdere il valore formativo dell’insegnamento della matematica è il rischio a cui sta andando incontro la società e la scuola di oggi, abbracciando posizioni estreme che si potrebbero esprimere citando un influente esperto americano di educazione, Abraham Flexner, in un articolo del 1916 − ma purtroppo attualissimo! −, “A modern school”: “Se, per esempio, fosse insegnato solo quel tanto di aritmetica che la gente ha effettivamente opportunità di usare, la matematica si ridurrebbe a proporzioni modeste. […] La stessa politica deve essere impiegata per quanto riguarda l’algebra e la geometria. Ciò che è insegnato, quando è insegnato e come è insegnato dipenderà quindi completamente da ciò di cui v’è bisogno, da quando ve n’è bisogno e della forma in cui ve n’è bisogno”.

Ma “la matematica non è un insieme di ricette circoscritte in termini funzionali. La matematica è una complessa “cassetta di idee e strumenti concettuali” molto specifici che deve essere continuamente arricchita attraverso la soluzione di problemi”, come affermano ancora gli autori di Pensare in matematica.

“Guardi, mio figlio e la matematica…”, “non è portato per la matematica, ha preso dalla madre…”, “ha avuto problemi fin dalla scuola elementare…”, “ha avuto un professore alle medie che non spiegava mai, gliel’ha fatta odiare…”, “si impegna tanto ma più di così…”: sono solo alcune delle osservazioni comuni nel corso dei colloqui con i genitori di un docente di matematica della scuola media superiore.

Le difficoltà in matematica nel nostro paese allora si possono ricondurre ad una didattica della disciplina che si è ridotta a trasmissione di ricette, regole o formule da applicare.

Si dice che un ragazzo è portato o non è portato, ma il verbo “portare” che soggetto ha? Chi porta uno studente alla matematica? Per rispondere a questa domanda e non solo ci viene ancora in aiuto George Polya: “la preparazione degli insegnanti di matematica della scuola media è insufficiente. […] La nostra conoscenza di ogni materia consiste di informazioni e del ‘sapere come‘. […] in matematica, il “saper come” è molto più importante che il solo possedere delle informazioni. […] l’insegnante dovrebbe sviluppare il ‘saper come’ dei suoi studenti, la loro abilità a ragionare; dovrebbe riconoscere ed incoraggiare il pensiero creativo − ma il curriculum attraverso cui è passato ha prestato attenzione insufficiente alla sua padronanza della materia e nessuna attenzione affatto al suo ‘saper come’, alla sua abilità a ragionare, alla sua abilità a risolvere problemi, al suo pensiero creativo”.

La questione dunque riguarda noi insegnanti, la nostra formazione, non nascondiamoci dietro al cambiamento dei nostri allievi, delle nuove generazioni. “Se l’insegnante non ha avuto alcuna esperienza nel lavoro creativo di qualche tipo, come potrà ispirare, guidare, aiutare o anche solo riconoscere l’attività creativa dei suoi studenti? Un insegnante che ha acquisito tutto quello che sa di matematica in modo puramente ricettivo, difficilmente può promuovere l’apprendimento attivo degli studenti. Un insegnante che non ha mai avuto un’idea brillante nella sua vita rimprovererà probabilmente uno studente che ne ha una, invece di incoraggiarlo”.

Personalmente credo che non si debba mai smettere di studiare come non si smette mai di imparare, ma per quanto riguarda la matematica studiare non è più solamente un’opzione, è un obbligo! Non può insegnare la matematica chi non la sa. Sembra una banalità, ma è quanto scoprono le maestre della scuola primaria, i docenti della scuola secondaria di primo grado laureati in Biologia, Chimica, Fisica, Scienze Naturali, ecc…, quando si trovano di fronte alla bellissima fatica dell’insegnamento di questa disciplina. Sembra una situazione senza speranza, ma nella realtà della nostra scuola ci sono anche molte persone disposte a mettersi a studiare per colmare le proprie lacune e che ogni giorno entrano in classe accettando la sfida di un insegnamento capace di coinvolgere i loro allievi, di destare il loro interesse.

Sono sorte associazioni di insegnanti specializzati e con esperienza che non si arrendono ad una scuola che sta diventando un’arida e vuota trasmettitrice di nozioni ma, rispondendo al desiderio di chi vuole approfondire la propria disciplina, si coinvolgono in progetti formativi e d’eccellenza. Certamente non si tratta di insegnare ad insegnare: ancora Polya affermava che “quello che l’insegnante insegna non è mai meglio di quello che è l’insegnante − l’insegnamento dipende completamente dalla personalità dell’insegnante − esistono tanti buoni metodi quanti sono i bravi insegnanti”.

Occorre, però, prendere seriamente in considerazione la questione sull’attuale carenza di formazione dei docenti di matematica: chi insegna ai futuri insegnanti − continuava ancora Polya − “dovrebbe aver fatto un po’ d’esperienza, seppur modesta, di ricerca matematica. Se non ha avuto un’esperienza di tale tipo, come potrebbe trasmettere quella che dovrebbe essere la cosa più importante per i futuri insegnanti, cioè lo spirito del lavoro creativo?”. Quindi attività di ricerca matematica ed esperienza di insegnamento sul campo dovrebbero essere le qualità richieste a chi tiene i corsi abilitanti (Tfa, Pas…).

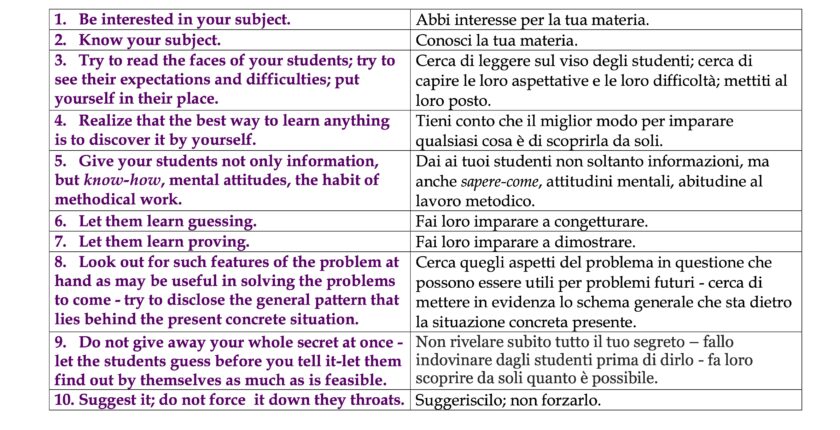
Mi permetto di concludere queste osservazioni ancora con un contributo di Polya che si potrebbe applicare a qualsiasi situazione d’insegnamento, a qualsiasi materia, insegnata a qualsiasi livello: si tratta dei “dieci comandamenti dell’insegnamento”, da leggere come un consiglio da giudicare e da sperimentare nella propria situazione particolare.

1. Abbi interesse per la tua materia.

2. Conosci la tua materia.

3. Conosci i modi secondo i quali si impara: il miglior modo per imparare qualsiasi cosa è di scoprirla da soli.

4. Cerca di leggere sul viso degli studenti, cerca di capire le loro aspettative e le loro difficoltà; mettiti al loro posto.

5. Dai loro non soltanto informazioni, ma anche “saper-come”, attitudini mentali, abitudine al lavoro metodico.

6. Fai loro imparare ad indovinare.

7. Fai loro imparare a dimostrare.

8. Cerca quegli aspetti del problema in questione che possono essere utili per i problemi futuri – cerca di mettere in evidenza lo schema generale che sta dietro la situazione concreta presente.

9. Non rivelare subito tutto il tuo segreto – fallo indovinare dagli studenti prima di dirlo – fa loro scoprire da soli quanto è possibile.

10. Suggeriscilo, non forzarlo.

Dunque bisogna “costruire progetti educativi incentrati sull’interesse”? Non saprei, direi piuttosto che c’è bisogno di insegnanti, cioè di uomini con tre passioni: passione per sé, passione per la propria disciplina, passione per le persone (siano esse colleghi o studenti).

Luigi Regoliosi (26 marzo 2014, IlSussidiario.net)