“Chiodo chiama martello”

Uno dei più grandi problemi nella didattica delle matematica è l’uso delle formule. Da un lato semplificano i problemi, dall’altro però limitano la libertà e la fantasia degli alunni, impedendo loro di fare una vera esperienza formativa con la disciplina.
Dal punto di vista dell’insegnante poi la formula come unica strategia risolutiva è spesso sinonimo di tranquillità e di sicurezza perché gli permette di non incontrare “difficoltà impreviste” durante la correzione o durante le normali lezioni. Questo accade in tutte le ramificazioni della matematica, dall’aritmetica alla geometria, dall’algebra polinomiale alle equazioni di ogni ordine e grado.
Il nostro motto – anche se in realtà sarebbe quello della Matematica – è quello di invitare i nostri studenti a GUARDARE, insieme a noi, quello che hanno davanti e non ad ESEGUIRE A TESTA BASSA!!
Per mostrare la nostra visione didattica, per cui non esistono “casistiche”, illustriamo la legge non scritta
CHIODO CHIAMA MARTELLO:
se devo piantare un chiodo (risolvere un problema) e possiedo una cassetta degli attrezzi (i contenuti/strumenti matematici acquisiti), non prendo un attrezzo a caso dalla cassetta, ma so già che devo prendere un martello; così come se ho una vite da avvitare prendo il cacciavite… In ogni caso, non sarebbe ragionevole prendere dalla cassetta diversi attrezzi per trovare quello giusto, ovvero prendere le tenaglie, il cacciavite, ecc, per provare a piantare il chiodo e rendersi conto, solo alla fine, che l’unico in grado di piantare adeguatamente il chiodo è proprio il martello! Sottolineiamo l’avverbio “adeguatamente” perché a volte si riesce a piantare un chiodo anche con un cacciavite, ma non viene dritto come con il martello! “Pensare in matematica” vuol dire riconoscere già nella richiesta del problema l’attrezzo giusto per risolverlo!
Per dettagliare meglio come abbiamo affrontato tale questione proponiamo due esempi riguardanti la risoluzione di un’equazione di secondo grado, uno meno convenzionale e un altro più noto.
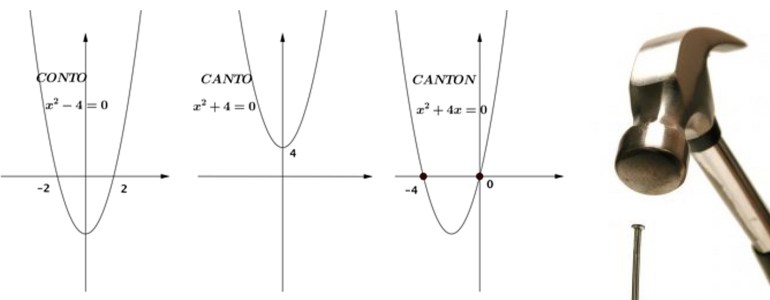
Il primo esempio riguarda la distinzione tra equazioni binomie di secondo grado simili ma diverse. Tale questione – di fronte alla quale si è trovato qualunque docente di scuola secondaria superiore – è stata affrontata per la prima volta in una classe di liceo classico che non voleva saperne di imparare a distinguere tali equazioni. Dopo una notte insonne, un nostro docente ebbe la seguente illuminazione: perché non provare con l’analogia con parole simili ma diverse come CONTO, CANTO e CANTON?
Assoceremo dunque a ciascuna di queste parole un’equazione:

$latex CONTO \Rightarrow x^2-4=0$
$latex CANTO \Rightarrow x^2+4=0$
$latex CANTON\Rightarrow x^2+4x=0$

Come le parole che hanno una sola lettera diversa (CONTO e CANTO) o una in più (CANTON e CANTO), anche le tre equazioni hanno solamente un segno diverso $latex (x^2-4=0)$ e $latex (x^2+4=0)$ o una $latex x$ in più $latex (x^2+4=0)$ e $latex (x^2+4x=0).$
Cosa comportano queste osservazioni ai fini della risoluzione delle tre equazioni?

CONTO si risolve contando, ovvero:
$latex x^2=4\Rightarrow x=\pm \sqrt{4}=\pm 2$

CANTO si risolve cantando, ovvero senza nessun calcolo, poiché una somma di numeri positivi non può essere mai uguale a zero.

CANTON si risolve raccogliendo a fattor comune la $latex x$ (la N di CANTON!), ovvero
$latex x(x+4)=0 \Rightarrow x_1=0$ e $latex x_2=-4$

Il secondo esempio – più famoso – riguarda il cosiddetto trinomio SPeciale, o Somma e Prodotto.
Consideriamo il trinomio di secondo grado $latex x^2+bx+c, (a=1),$ poiché tutti gli altri sono riconducibili ad esso.
Si tratta di riconoscere che ogni polinomio di secondo grado riducibile, ovvero che ammette soluzioni reali $latex x_{1}$ e $latex x_{2},$ può essere riscritto nel seguente modo:
$latex x^2+bx+c=(x-x_{1})(x-x_2)$
E dunque ecco perché Somma e Prodotto:
$latex x^2+bx+c=x^2-(x_1+x_2)\cdot x+x_1\cdot x_2,$
o più semplicemente
$latex x^2-sx+p,$
dove $latex s$ è la somma delle due soluzioni e $latex p$ è il prodotto.
Vediamolo in un paio di esempi:
1) devo risolvere
$latex x^2-5x+6=0$
Facilissimo! La somma è 5 e il prodotto è 6. Si inizia sempre dal prodotto: si tratta di trovare due numeri il cui prodotto dia come risultato 6 e la somma 5, trovati???
2) devo risolvere
$latex x^2-8x+16=0$
In questo caso particolare la somma è 8 e il prodotto è 16. Evidentemente le due soluzioni sono coincidenti e valgono lo stesso numero: si tratta, infatti, del quadrato del binomio $latex (x-4)^2…$
Solamente un paio di osservazioni conclusive: anzitutto non bisogna commettere l’errore di pensare che le equazioni di secondo grado da proporre siano solamente quelle con soluzioni reali non intere, in cui va applicata “per forza” la formula risolutiva (sebbene pure in tale situazione avremmo il metodo alternativo del completamento del quadrato, anch’esso quasi assente nella scuola attuale). Spesso gli studenti, infatti, sono così abituati ad ottenere soluzioni stravaganti, che i più “studiosi” risolvono anche le più semplici con la formula, mentre i più “lacunosi” non risolvono neanche quelle perché spaventati dall’idea di dover trattare numeri irrazionali!  La formula risolutiva, dunque, può essere utilizzata tutte le volte, ma è d’obbligo solo nel caso in cui le soluzioni non sono evidenti e non si riescono a trovare rapidamente le soluzioni.
L’ultima considerazione è dedicata ai due possibili motivi (uno nobile e uno meno nobile) per cui, alla fine, usiamo la formula risolutiva:
1) non ci sono soluzioni reali oppure non sono entrambe intere;
2) non vogliamo pensare, ma solo eseguire per arrivare ad una soluzione!
Buona Matematica a chi vuol capire e far fatica, tenendo alta la testa e non semplicemente eseguendo a testa bassa!